
Расчёт равновесного уровня национального дохода
В экономике страны «А» функция инвестиций описывается уравнением
I = 40 + 0,4Y,
а функция сбережений
S = – 20 + 0,6Y,
где Y – величина национального дохода.
Определите равновесный уровень национального дохода.
Решение:
Тождество сбережений и инвестиций в закрытой экономике, в которой отсутствует государственный сектор, а следовательно, налоги и трансферты имеет вид:
Расходы на ВНП = Потребление + Инвестиции
или в буквенном обозначении:
Y = C + I
Доход, или ВНП, измеренный по доходам = Сбережения + Потребление
или
Y = S + C
Т.к. расходы на ВНП и доходы, полученные в результате производства ВНП, равны, то приравнивая уравнения, имеем:
C + I = S + C
или
I = S
40 + 0,4Y = – 20 + 0,6Y
0,2Y = 60
Y = 300
Расчёт потоков перемещения денежных средств
Кругооборот расходов и доходов в открытой экономической системе характеризуется следующими потоками:
| заработная плата | 1000 |
| амортизация | 75 |
| чистые частные внутренние инвестиции | 300 |
| экспорт товаров и услуг | 100 |
| зарубежные инвестиции | 50 |
| импорт товаров и услуг | 150 |
| нераспределенная прибыль корпораций | 5 |
| дивиденды | 60 |
| потребительские расходы домохозяйств | 700 |
| пенсии, стипендии, пособия | 200 |
| подоходные налоги | 350 |
| налоги на прибыль корпораций | 100 |
| государственные закупки товаров и услуг | 210 |
Рассчитав потоки перемещения денежных средств между различными секторами экономики, заполните следующую таблицу:

Решение:
Приращение имущества предпринимателей в текущем периоде составило 45, домашних хозяйств — 210, государства — 40.

Расчёт коэффициента Джини
Предположим, что в некоторой стране N проживают три группы населения: бедные, средний класс и богатые. Группы равны по численности жителей, но различаются по уровню дохода: средний класс зарабатывает в два раза больше, чем бедные, а богатые зарабатывают в два раза больше, чем средний класс. Внутри групп доходы распределены равномерно. Совокупный доход всех жителей страны равен Y. Нарисуйте график кривой Лоренца и рассчитайте индекс Джини.
Решение:
Третья часть населения, по условию задачи, бедные. Их доходы обозначим через х.
Тогда 2х – величина доходов среднего класса,
4х — величина доходов богатых.
Следовательно, совокупный доход всех жителей страны Y состоит из 7 одинаковых частей.
1/7 – доля доходов бедных,
2/7 – доля доходов среднего класса,
4/7 – доля доходов богатых.
Представим условие задачи в табличной форме:

Индекс Джини рассчитаем двумя способами.
1) Способ аналитический. Коэффициент Джини рассчитывается по формуле:
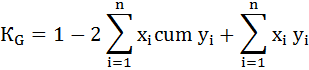
где
xi – доля населения, принадлежащая к i-й социальной группе в общей численности населения;
уi – доля доходов, сосредоточенная у i-й социальной группы населения;
n – число социальных групп;
cum yi – кумулятивная доля дохода.
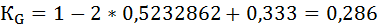
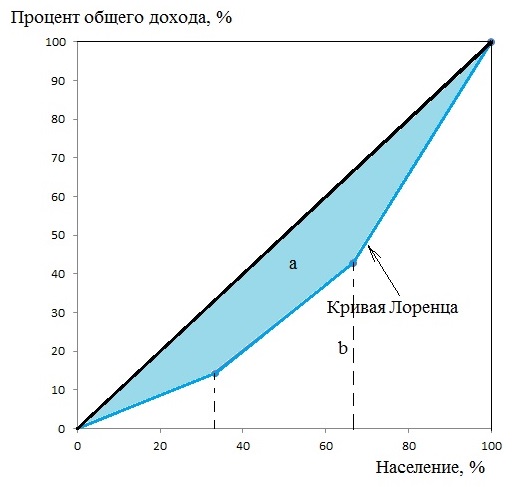
2) Способ геометрический. Коэффициент Джини определяется как отношение площади фигуры, образуемой кривой Лоренца и линией равномерного распределения (Sa), к площади треугольника ниже линии равномерного распределения (Sa+b):
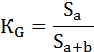
Площадь фигуры, образуемой кривой Лоренца и линией равномерного распределения (Sa) легко найти вычитанием из площади треугольника (Sa+b) площадь фигуры, лежащей ниже кривой Лоренца.
Площадь фигуры b, лежащей ниже кривой Лоренца можно разбить на треугольник и две трапеции:
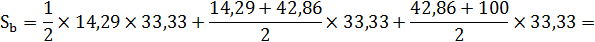
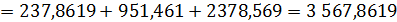
Площадь фигуры a будет равна:
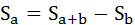
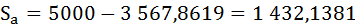
Индекс Джини будет равен:
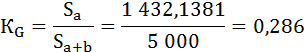
Оба способа дали одинаковый результат.
Как видно из таблицы, наиболее обеспеченная группа населения сконцентрировала 57,14% доходов, а доля наименее обеспеченной группы в общем доходе составила 14,29%.
Расчёт коэффициента Джини
В стране N число домашних хозяйств разделено на две группы:
первая группа населения (60 %) имеет низкие доходы, составляющие 45 % всех доходов;
вторая группа получает 55 % доходов.
Рассчитайте коэффициент Джини. Какова степень социально-экономического расслоения доходов?
Решение:
Построим кривую Лоренца, с помощью которой рассчитаем коэффициент Джини.
Кривая Лоренца иллюстрирует степень неравномерности в распределении доходов. При равномерном распределении доходов каждая 20% -я группа населения имеет пятую часть доходов общества. На графике это изображается диагональю квадрата АВ, что означает равномерное распределение. При неравномерном распределении «линия концентрации» представляет собой вогнутую вниз кривую. В данной задаче это кривая АСВ.
Чем больше отклонение кривой Лоренца от диагонали квадрата, тем выше поляризация доходов общества.
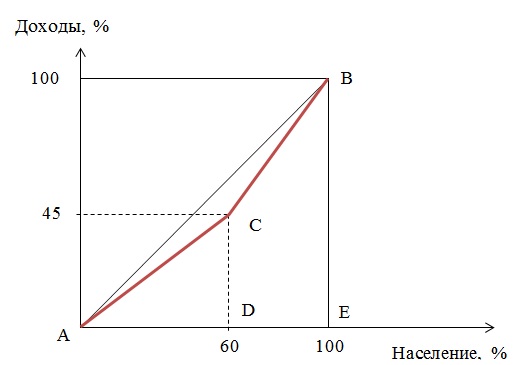
Коэффициент Джини можно рассчитать по кривой Лоренца как отношение площади фигуры, образуемой кривой Лоренца и линией равномерного распределения (ΔАВС), к площади треугольника ниже линии равномерного распределения (ΔАВЕ).
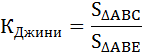
Площадь ΔАВС определим вычитанием из площади ΔАВЕ площади фигуры АСВЕ, расположенной под кривой Лоренца, которая состоит из площади треугольника ΔАСD и площади трапеции DCBE.
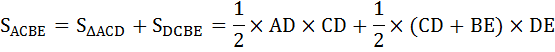
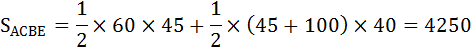
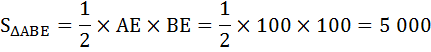
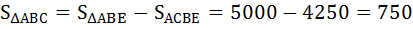
Рассчитаем коэффициент Джини:
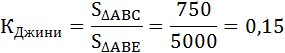
Что говорит о низкой степени социально-экономического расслоения доходов.



