
Задача №1. Определение изменения дохода при увеличении проданной продукции на одну единицу
Фирма имеет кривую спроса:
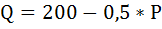
Зная, что P=100, определить изменение дохода при увеличении проданной продукции на одну единицу.
Решение:
Прирост дохода при увеличении проданной продукции на одну единицу называют предельной выручкой (MR — marginal revenue).
Предельная выручка может быть представлена как частная производная общей выручки по количеству товара.
Кроме того цена и объём связаны между собой функциональной зависимостью: Р = f(Q).
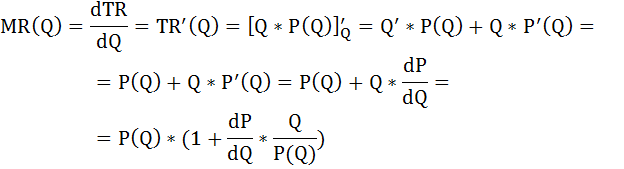
Легко заметить, что второе слагаемое в скобках есть обратное значение эластичности спроса:
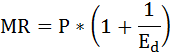
Определим эластичность спроса по цене:
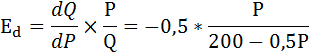
При P=100
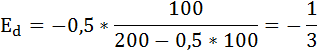
Тогда:
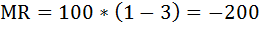
Таким образом, увеличение количества проданной продукции на единицу, уменьшит доход фирмы на 200 единиц.
Задача №2. Коэффициент точечной эластичности
Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.
а) Как изменилась выручка фирмы?
б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.
Решение:
а) Выручка фирмы рассчитывается по формуле:
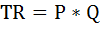
Соответственно изменение выручки фирмы в процентном выражении рассчитаем по формуле:
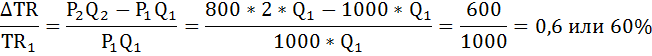
Таким образом, выручка фирмы увеличилась на 60 %.
б) Коэффициент точечной эластичности рассчитаем по формуле, используемой в определении:
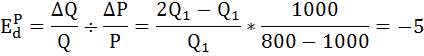
Коэффициент эластичности по абсолютной величине больше 1, следовательно спрос эластичен.
Задача №3. Эластичность спроса по цене
Функция задана уравнением
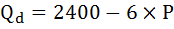
а) Выведите формулу эластичности этого спроса.
б) При какой цене эластичность спроса по цене составит – 0,5?
в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?
Решение:
а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.
В точке (P0,Q0) точечная эластичность вычисляется как
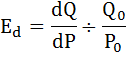
Где
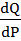
– производная функции спроса в этой точке.
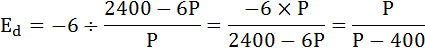
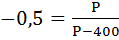
б)
Отсюда:
Р = 133,33
в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.
Задача №4. Функция суммарного спроса
а) Определить функцию суммарного спроса на основании данных об индивидуальном спросе:
Q(1) = 100 – 5 P при P≤ 20 и 0 при Р > 20,
Q(2) = 50 – 8 P при P≤ 10 и 0 при Р > 10,
Q(3) = 56 – 4 P при P≤ 14 и 0 при Р > 14.
б) Найти эластичность спроса в точке P = 12.
Решение:
а) Для определения функции суммарного спроса при каждом возможном уровне цены необходимо сложить величины индивидуальных спросов отдельных покупателей.
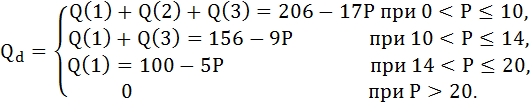
б) Так как точка P=12 находится в промежутке [10;14], то эластичность спроса в этой точке найдём для функции
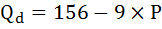
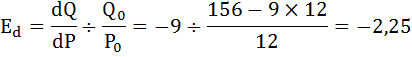
Так как абсолютное значение коэффициента эластичности больше единицы, следовательно спрос эластичен.
Задача №5. Функция суммарного спроса
Известны данные об индивидуальном спросе:
Q(1) = 80 – 8 P при P ≤ 10 и 0 при Р > 10,
Q(2) = 50 – 10 P при P ≤ 5 и 0 при Р > 5,
Q(3) = 32 – 4 P при P ≤ 8 и 0 при Р > 8.
а) Выведите уравнение кривой спроса аналитически.
б) Получите формулу эластичности по абсолютной величине в зависимости от цены.
Решение:
а) Для определения функции суммарного спроса при каждом возможном уровне цены необходимо сложить величины функций индивидуального спроса отдельных покупателей.
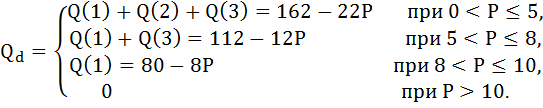
Формула эластичности для непрерывной функции выглядит следующим образом:
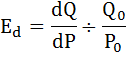
Тогда эластичность для каждой функции спроса по абсолютной величине будет равна:
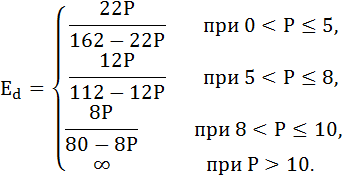
Задача №6. Расчёт дуговой эластичности
Является ли спрос на товар эластичным, если известно:
| Цена, руб. | Объём спроса |
|---|---|
| 3500 | 500 |
| 4000 | 440 |
Решение:
При значительных колебаниях цены (более 10%) рекомендуется использовать коэффициент дуговой эластичности:
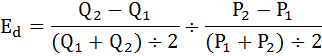
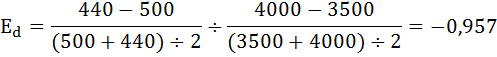
Так как:
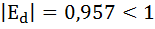
значит спрос на товар не эластичен.
Задача №7. Расчёт дуговой эластичности
Является ли спрос на товар эластичным, если известно:
| Цена, руб. | Величина спроса | Объём продаж |
|---|---|---|
| 500 | 300 | 150 |
| 700 | 240 | 220 |
Решение:
Чтобы ответить на вопрос задачи необходимо рассчитать коэффициент дуговой эластичности по формуле:
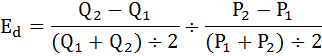
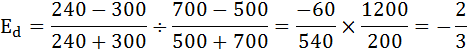
Так как:
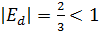
следовательно спрос на товар не эластичен.
Задача №8. Расчёт точечной эластичности
Определить точечную эластичность спроса, если при снижении цены на 10 % выручка увеличилась на 8 %.
Решение:
Пусть P– первоначальная цена до её снижения, а Q– величина спроса до снижения цены.
Тогда выручка будет равна:
PQ.
Из условия задачи известно, что цена снизилась на 10%, запишем это как:
ΔP / P = -0,1
А выручка увеличилась на 8%, то есть стала равна:
1,08PQ
По-другому выручку после изменения можно записать как:
0,9P(Q + ΔQ)
Приравняв два последних выражения, получим уравнение:
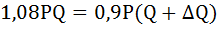
Разделим обе части уравнения на PQ
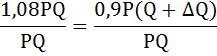
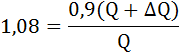
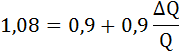
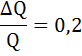
Рассчитаем точечную эластичность спроса по формуле
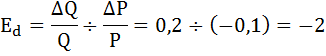
Так как коэффициент точечной эластичности по абсолютной величине больше единицы, следовательно спрос эластичен.
Задача №9. Расчёт точечной эластичности
Определить точечную эластичность спроса на товар, если уменьшение цены на 5 % привело к снижению выручки на 2 %.
Решение:
Пусть P– первоначальная цена до её уменьшения,
а Q– величина спроса до уменьшения цены.
Тогда выручка будет равна PQ.
Из условия задачи известно, что цена снизилась на 5%, запишем это как:
ΔP / P = -0,05
А выручка снизилась на 2%, то есть стала равна:
0,98PQ
По-другому выручку после изменения можно записать как:
0,95P(Q+ΔQ)
Приравняв два последних выражения, получим уравнение:
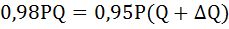
Разделим обе части уравнения на PQ
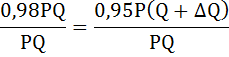
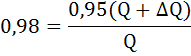
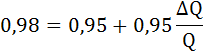
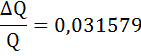
Рассчитаем точечную эластичность спроса по формуле:
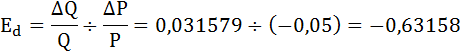
Так как коэффициент точечной эластичности спроса по абсолютной величине меньше единицы, следовательно, спрос неэластичен.
Задача №10. Расчёт первоначального объёма рыночного спроса
Цена за товар выросла с 30 до 33 рублей. Точечная эластичность спроса на него при цене 30 руб. равна (-2). Каков был первоначальный объём рыночного спроса на этот товар, если после повышения цены он составил 1200 единиц.
Решение:
Точечная эластичность спроса рассчитывается по формуле:
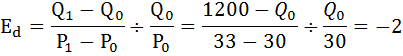
Отсюда:
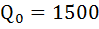
.



