Микроэкономика. Анализ рыночной структуры. Задачи.

Задача №1. Расчёт экономической прибыли конкурентной фирмы

Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат:

ТС = 140 + 10 × Q + 40 × Q².

При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы.

Будут ли в длительном периоде в эту отрасль стремиться войти новые фирмы?

Решение:

Наличие  в составе общих затрат фиксированных (постоянных) затрат (FC = 140) свидетельствует о том, что речь идёт о краткосрочном периоде.

Найдём объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде имеет вид:

Р = МС = МR = AR.

Определим функцию предельных издержек фирмы: найдём производную общих издержек.

МС = (ТС)’ = 10 + 80 × Q.

Приравняем эту функцию к цене равной 250.

10 + 80 × Q = 250

80 × Q = 240

Q = 3

Вычислим прибыль фирмы при объёме выпуска равном 3 по формуле:

П = TR — TC = P × Q — TC = 250 × 3 — (140 + 10 × 3 + 40 × 3²) = 220 ден. ед.

В долгосрочном периоде наличие неотрицательной экономической прибыли будет привлекать в отрасль новые фирмы.

Задача № 2. Определение рыночной цены и отраслевого выпуска продукции

В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями

ТС =Q³ — 36*Q² + 384*Q,

где

Q — объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие.

Решение:

В долгосрочном периоде на рынке совершенной конкуренции соблюдается равенство:

P = MC = MR = AR = minAC.

Найдём функцию средних издержек каждой фирмы по следующей формуле:

АС = ТС / Q = Q² — 36*Q + 384

Далее необходимо найти минимум данной функции. Для этого определим производную функции АС и приравняем её к нулю.

2*Q — 36 = 0

Q = 18

AC(18) = 18² — 36*18 + 384 = 60

Так как Р = minAC в долгосрочном периоде, следовательно, рыночная цена равна Р = 60.

Найдём отраслевой выпуск. Так как каждая из фирм отрасли производит 18 тысяч штук продукции, значит 130 фирм произведут:

Q_отр. = 18*130 = 2340 тысяч штук

Задача № 3. Определение рыночной цены в долгосрочном периоде

Конкурентная фирма находится в состоянии равновесия в долгосрочном периоде и имеет следующие затраты: TC = Q³ — 38*Q² + 418*Q. Определите цену на этом рынке в долгосрочном периоде.

Решение:

В долгосрочном периоде цена в условиях соверешенной конкуренции устанавливается на уровне минимума средних затрат. При этом фирма совершенный конкурент получает нулевую экономическую прибыль.

Условие равновесия на рынке будет иметь вид:

Р = МС = МR = AR = min AC

Найдём средние затраты фирмы по формуле:

АС = ТС / Q = Q² — 38*Q + 418

Определим минимум функции средних затрат. Для нахождения экстремума функции  приравняем к нулю её производную:

АС’ = 2*Q — 38

2*Q — 38 = 0

Q = 19

При выпуске Q = 19 средние затраты будут равны:

АС = 19² — 38*19 + 418 = 57.

Таким образом, цена в долгосрочном периоде будет равна 57.

Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка

Общие затраты фирмы, действующей на рынке совершенной конкуренции, составляют

0,5*Q³ — 15*Q² + 300*Q + 250 000.

При какой цене фирме становится невыгодным работать на этом рынке в краткосрочном периоде?

Решение:

В краткосрочном периоде фирма совершенный конкурент уйдёт с рынка, если цена окажется меньше  минимума её средних переменных издержек: Р < min AVC.

Найдём переменные издержки фирмы, а точнее запишем функцию переменных издержек:

VC = 0,5*Q³ — 15*Q² + 300*Q

Теперь определим функцию средних переменных издержек  по формуле:

АVC = VC / Q = 0,5*Q² — 15*Q + 300

Найдём экстремум этой функции, приравняв к нулю её производную.

Q — 15 = 0

Q = 15.

При объёме производства Q = 15 средние переменные издержки будут минимальными.

АVC(15) = 0,5*15² — 15*15 + 300 = 187,5

Это так называемая точка закрытия фирмы. Фирма совершенный конкурент уйдёт с рынка, если цена упадёт ниже этой точки в краткосрочном периоде.

При Р < 187,5 фирме становится невыгодным работать на этом рынке в краткосрочном периоде.

Задача № 5. Расчёт объёма выпуска, максимизирующего прибыль фирмы

Функция издержек фирмы ТС = Q² — Q + 3, где Q — объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы.

Решение:

По условию рыночная цена не зависит от объёма продаж этой фирмы, это говорит о том, что фирма функционирует в условиях совершенной конкуренции.

Максимум прибыли фирмы действующей в условиях совершенной конкуренции определяется тождеством: Р = МС.

Найдём предельные издержки фирмы по формуле:

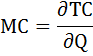
МС =(TC)’= 2Q — 1

Найдём объём выпуска продукции, максимизирующий прибыль фирмы.

Цена по условию равна Р = 7.

Р = МС

7 = 2Q — 1

Q = 4

Задача №6. Расчёт объёма производства в краткосрочном периоде

В отрасли совершенной конкуренции установилась цена Р = 30. В эту отрасль входит фирма с общими издержками ТС = 1/2 * Q² + 10 * Q + 100. Найти её объём производства в краткосрочном периоде.

Решение:

Фирма выберет такой объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли: МС = MR.

На рынке совершенной конкуренции предельный доход равен цене: MR = P.

Отсюда следует, что цена равна предельным издержкам: P = MC.

Найдём предельные издержки. Предельные издержки в непрерывном случае (т.е. когда общие издержки заданы функцией) равны производной от функции общих издержек:

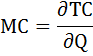
Функция предельных издержек будет иметь вид:

МС = Q + 10
P = MC
30 = Q + 10
Q = 20 — оптимальный объём производства фирмы.

Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет общие затраты

ТС = 800 + 40*Q + 2*Q²

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли фирмы имеет вид:

П = TR — TC = P*Q — TC

По условию максимально возможная прибыль равна 1000.

P*Q — (800 + 40*Q + 2*Q²) = 1000

Найдём цену.

Условие максимизации прибыли на рынке совершенной конкуренции имеет вид:

Р = МС = MR = AR

Так как Р = МС, а МС = ТС’ = 40 + 4*Q, следовательно, Р = 40 + 4*Q. Подставим это выражение в формулу прибыли и получим:

(40 + 4*Q)*Q — (800 + 40*Q + 2*Q²) = 1000

40*Q + 4*Q² — 800 — 40*Q — 2*Q² — 1000 = 0

2*Q² = 1800

Q² = 900

Q_1,2 = ±30

Так как отрицательный корень экономического содержания не имеет, берём Q = 30.

Тогда цена будет равна:

Р = 40 + 4*30 = 160

Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде

Допустим, общие затраты фирмы на выпуск Q единиц продукции составляют:

Q³ – 16*Q² + 400*Q.

а) При каком значении Q средние затраты достигают минимума?

б) При какой цене этой фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде?

Решение:

а) Найдём функцию средних затрат по формуле:

АС = ТС / Q = (Q³ – 16*Q² + 400*Q) / Q = Q² – 16*Q + 400

Определим минимум функции. Для нахождения экстремума функции необходимо найти её производную и приравнять её к нулю.

AC’ =(Q2 – 16*Q + 400)’ = 2*Q – 16
2*Q – 16 = 0
Q = 8

При Q = 8 средние затраты достигают минимума.

б) В долгосрочном периоде фирме становится выгодным участвовать в совершенной конкуренции, если Р ≥ АС. При этом фирма имеет нулевую прибыль. И выполняется условие:

Р = МС = MR = minАС

Рассчитаем minAC. Подставим Q = 8 в функцию средних затрат:

minAC(Q=8) = 82 – 16*8 + 400 = 336

Итак, при цене Р ≥ 336 фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде.

Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль

Спрос на продукцию конкурентной отрасли:

Q_d = 55 – P

Предложение:

Q_s = 2P – 5

Если у одной из фирм отрасли восходящий участок кривой предельных издержек:

МС = 3Q + 5

При каких цене и объёме производства фирма максимизирует прибыль?

Решение:

Найдём цену равновесия. Приравняем функцию спроса и предложения:

Qd = Qs
55 – P = 2P – 5
3 * Р = 60
Р = 20 – цена рыночного равновесия, то есть цена по которой фирмы будут продавать свою продукцию.

Фирма в условиях совершенной конкуренции получает максимум прибыли при условии равенства цены и предельных затрат.

МС = Р
3Q + 5 = 20
Q = 5 – объём производства, при котором прибыль фирмы будет максимальной.

Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет предельные затраты:

МС = 30 + 2 × Q

при фиксированных затратах, равных 500 денежным единицам.

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1100 денежным единицам.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли имеет вид:

П = TR – TC = P*Q – TC

Определим функцию общих затрат. Так как функция предельных затрат это производная функции общих затрат, следовательно, функцию общих затрат можно определить как первообразную от функции предельных затрат.

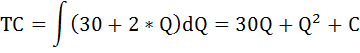
где

С – константа, равная величине фиксированных затрат, которые по условию равны 500.

Таким образом функция общих затрат имеет вид:

ТС = Q² +30*Q + 500

Теперь запишем условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде:
Р = МС = MR = AR

Воспользуемся тем, что:

Р = МС

По условию задачи:

МС = 30 + 2 × Q, то есть Р = 30 + 2 * Q

Подставим это выражение, а так же функцию общих затрат в формулу прибыли и получим уравнение с одной неизвестной.

(30 + 2 * Q) * Q – (Q² +30*Q + 500) = 1100
Q2 = 1600
Q = ± 40

Так как отрицательное значение Q экономического смысла не имеет, следовательно, объём выпуска данной фирмы Q = 40.

Тогда рыночная цена будет равна:

Р = 30 + 2 * 40 = 110.