Микроэкономика. Рынки факторов производства. Задачи.

Задача № 1. Расчёт цены земли

На четырех одинаковых по площади земельных участках выращивается виноград.Природно-экономические показатели этих земель характеризуют следующие данные:

Участок	I	II	III	IV
Расходы выращивания, грн.	2000	2600	3600	4000
Валовой сбор, т	8	12	20	16
Расстояние до рынка сбыта, км	10	50	100	105

Транспортный тариф перевозок 1 т на расстояние в 1 км 0,4

Величина абсолютной ренты, грн. 300.

Определите:

цену каждого участка, если известно, что общественная норма прибыли — 15%, а ссудный процент на одолженный у банка капитал равен 5% годовых.

Виды ренты способствуют формированию цен на землю?

Существует ли дифференциальная рента на I участке?

Существует ли дифференциальная рента на II участке?

Какие участки обеспечивают этот вид ренты?

Назовите причины которые, на ваш взгляд обусловливают разное качество каждого земельного участка?

Участки имеют большую производительность?

Ответы обоснуйте экономичным анализом.

Решение:

В основе рыночных цен на сельскохозяйственную продукцию лежит стоимость единицы продукции, полученной с худших земельных участков. Поэтому вся продукция со всех земельных участков будет продаваться по цене, соответствующей стоимости продукции с худшего земельного участка. Худшим земельным участком будет тот, на котором затраты производства 1 т винограда самые высокие.

Для простоты анализа составим таблицу расчётных данных:

Участок земли	Издержки производства, грн.	Общественная нормы прибыли, %	Стоимость всей продукции, грн.	Валовый сбор, т	Абсолютная рента, грн.
А	1	2	3	4	5
I	2000 + 8 × 10 × 0,4 = 2032	15	2032 × 1,15 = 2336,8	8	300
II	2600 + 12 × 50 × 0,4 = 2840	15	2840 × 1,15 = 3266	12	300
III	3600 + 20 × 100 × 0,4 = 4400	15	4400 × 1,15 = 5060	20	300
IV	4000 + 16 × 105 × 0,4 = 4672	15	4672 × 1,15 = 5372,8	16	300

Издержки производства включают в данной задаче расходы выращивания и транспортные расходы.

Найдём цену земли.

Субъект, желающий купить земельный участок, должен учесть альтернативные варианты вложения денег и получения дохода. Субъект выбирает: положить деньги в банк или купить земельный участок. Поэтому при всех неизменных условиях цену земли можно выразить следующей формулой:

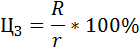
где

R – размер арендной платы (рента),
r – величина ссудного процента или процентная ставка,

Размер арендной платы = Абсолютная рента + Дифференциальная рента +

+ Процент на капитал

Так как в задании не сказано осуществлялись ли ранее капиталовложения в постройки и сооружения, размер арендной платы и размер совокупной ренты будут совпадать. В противном случае арендная плата на ряду с рентой включает в себя выплату процента на вложенный капитал и амортизационные отчисления на вложенный капитал.

Таким образом, для нашего задания:

Размер арендной платы = Абсолютная рента + Дифференциальная рента =

= Совокупная рента  

Абсолютная рента получается собственниками земли абсолютно со всех земельных участков и абсолютно одинаковой величины, если размеры земельных участков одинаковы.

В условии задания сказано, что все четыре участка одинаковы по площади и  величина абсолютной ренты равна 300 грн.

Дифференциальная рента будет получена собственниками земли только со средних и лучших участков земли, как по качеству и плодородию почвы, так и по месторасположению. Участки, обладающие дифференциальной рентой: I, II и III.

IV участок земли будет иметь только абсолютную ренту. Поэтому виды ренты будут способствовать формированию цен на землю. Цена земли IV участка будет зависеть только от величины абсолютной ренты и величины ссудного капитала, в отличии от I, II и III участка, где цена зависит ещё и от величины дифференциальной ренты.

Совокупная рента — это избыточная прибыль которую присваивают собственники земли.

Можно сказать, что собственник III участка, за счёт наилучшей его производительности получит наибольшую избыточную прибыль.

Рассчитаем цены земельных участков.

Цена I участка земли:

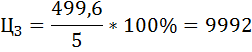
 грн.

Цена II участка земли:

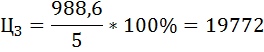
 грн.

Цена III участка земли:

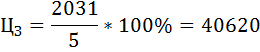
 грн.

Цена VI участка земли:

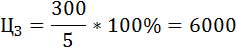
 грн.

Задача № 2. Выбор проекта для инвестирования

Имеется три проекта вложения денежных средств. Ставка процента составляет 15% годовых.

Рассчитать, какой проект является наиболее выгодным для инвестирования

Решение:

Для оценки будущих доходов при альтернативных вложениях капитала найдём текущую дисконтированную стоимость для каждого проекта по формуле:

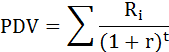
где

PDV – текущая дисконтированная приведённая стоимость,

R_i – доход от инвестиций в году t,

r – ставка процента.

Величина дисконтированного дохода проекта Зайка:

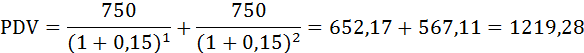
Величина дисконтированного дохода проекта Белочка:

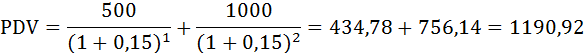
Величина дисконтированного дохода проекта Енотик:

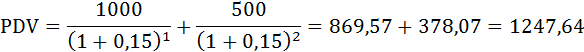
Итак, проект Енотик оказывается предпочтительнее для инвестирования.

Задача № 3. Расчёт оптимального выпуска продукции

Фирма находится в условиях совершенной конкуренции на рынке данного товара и труда. Ее производственная функция имеет вид

Q = 120 × L – 2 × L ²

в интервале использования труда от 12 до 30 единиц. Ставка заработной платы равна 60 ден. ед., а цена товара 8 ден. ед. Определить оптимальный для фирмы выпуск продукции.

Решение:

Общее условие максимизации прибыли при покупке фактора производства.

Для того чтобы получить максимальную прибыль произведя и продав продукцию на рынке готовой продукции фирма на рынке труда должна нанять такое количество работников, чтобы выполнялось следующее:

MRP_L = MIC

где

MRP_L – предельная доходность труда,

МIC – предельные издержки на фактор производства (труд).

MRP_L = MR × MP_L

где

MR – предельная выручка,

MP_L – предельный продукт труда.

Фирма находится в условиях совершенной конкуренции на рынке данного товара и на рынке труда.

Фирма, продающая продукцию на совершенно конкурентном рынке, не может повлиять на рыночную цену, она принимает её как заданную и в этом случае:

Р = МR

На рынке труда издержки фирмы на труд равны ставке заработной платы:

MIC = ω,

где

ω – ставка заработной платы

Таким образом, для совершенно конкурентной во всех отношениях фирмы условие максимизации прибыли при покупке фактора производства будет иметь вид:

P × MP_L = ω

Продифференцируем производственную функцию и найдём предельный продукт труда (MP_L) по формуле:

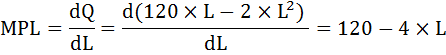
Подставим это выражение в условие максимизации прибыли и найдём количество нанимаемого труда:

8 × (120 – 4 × L) = 60

960 – 32 × L = 60

900 = 32 × L

L = 28,125

Оптимальный для фирмы выпуск продукции будет равен:

Q = 120 × 28,125 – 2 × 28,125 ² = 1793

Задача № 4. Расчёт количества закупаемого фактора

Фирма, являющаяся монополистом на рынке блага и совершенным конкурентом на рынке фактора, производит продукцию по технологии

Q = 2 × L.

Цена фактора 8 ден. ед. Функция спроса на продукцию монополиста

Qd = 12 – Р.

Определить количество закупаемого фактора, объем выпуска продукции и цену продукции, максимизирующие прибыль монополии.

Решение:

Общее условие максимизации прибыли при покупке фактора производства.

Для того чтобы получить максимальную прибыль произведя и продав продукцию на рынке готовой продукции фирма на рынке труда должна нанять такое количество работников, чтобы выполнялось следующее:

MRP_L = MIC_L

где

MRP_L – предельная доходность труда,

МIC_L – предельные издержки на фактор производства (труд).

MRP_L = MR × MP_L

где

MR – предельная выручка,

MP_L – предельный продукт труда.

Фирма является монополистом на рынке блага и совершенным конкурентом на рынке труда.

На рынке труда издержки фирмы на труд равны ставке заработной платы:

MIC = ω,

где

ω – ставка заработной платы

Таким образом, условие максимизации прибыли при покупке фактора производства будет иметь вид:

MR × MP_L = ω

Найдём предельную выручку как производную от общей выручки:

MR = TR’ = (P×Q)’ = (12 × Q – Q²)’=12 – 2 × Q

где

Р = 12 – Q – обратная функция спроса.

По условию Q = 2 × L, следовательно, MR = 12 – 4 × L

Найдём предельный продукт труда:

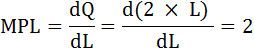
Воспользуемся условием максимизации прибыли и найдём количество закупаемого фактора :

(12 – 4 × L) × 2 = 8

L = 2

Тогда объем выпуска продукции Q = 4.

Цену продукции найдём из обратной функции спроса:

Р = 12 – Q =12 – 4 = 8

Задача № 5. Расчёт цены и количества труда

Фирма, являющаяся совершенным конкурентом на товарном рынке и монопсонистом на рынке фактора, производит продукцию по технологии

Q = 12 × L – 2 × L² .

Цена товара 5 ден. ед. Функция предложения труда имеет вид

L = 0,1 × ω – 2.

Определить, по какой цене фирма будет покупать труд, какое количество труда приобретет фирма, максимизирующая прибыль.

Решение:

Общее условие максимизации прибыли при покупке фактора производства.

Для того чтобы получить максимальную прибыль произведя и продав продукцию на рынке готовой продукции фирма на рынке труда должна нанять такое количество работников, чтобы выполнялось следующее равенство:

MRP_L = MIC_L 

где

MRP_L – предельная доходность труда,

МIC_L – предельные издержки на фактор производства (труд).

MRP_L = MR × MP_L

где

MR – предельная выручка,

MP_L – предельный продукт труда.

Фирма находится в условиях совершенной конкуренции на рынке данного товара и на рынке труда.

Фирма, продающая продукцию на совершенно конкурентном рынке, не может повлиять на рыночную цену, она принимает её как заданную и в этом случае:

Р = МR

На рынке труда предельные издержки фирмы монопсониста на труд равны:

MIC_L = (TIC_L)’ = (L × ω)’

По условию задачи известна функция предложения на труд

L = 0,1 × ω – 2,

отсюда

ω = 10 × L + 20

где

ω – ставка заработной платы,

L – количество нанимаемого труда.

MIC_L = (10 × L² + 20 × L)’ = 20 × L + 20

Таким образом, для фирмы, являющейся совершенным конкурентом на товарном рынке и монопсонистом на рынке труда условие максимизации прибыли при покупке фактора производства будет иметь вид:

P × MP_L = MIC_L

Найдём MP_L по формуле:

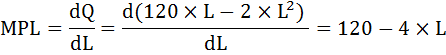
Воспользуемся условием максимизации прибыли и найдём количество труда, приобретаемое фирмой:

5 × (12 – 4 ) × L = 20 × L + 20

L = 1

Ставка заработной платы работника будет равна:

ω = 10 × 1 + 20 = 30

Задача № 6. Расчёт цены на продукцию фирмы

Фирма, являющаяся монополистом на рынке блага и монопсонистом на рынке труда, имеет производственную функцию

Q = 5 × L

функцию спроса на свою продукцию

Q_d = 100 – Р.

На рынке труд предлагается по формуле

L = 0,2 × ω – 4.

Определить, по какой цене фирма будет продавать продукцию при достижении максимума прибыли.

Решение:

Общее условие максимизации прибыли при покупке фактора производства.

Для того чтобы получить максимальную прибыль, произведя и продав продукцию на рынке готовой продукции, фирма на рынке труда должна нанять такое количество работников, чтобы выполнялось следующее:

MRP_L = MIC_L

где

MRP_L – предельная доходность труда,

МIC_L – предельные издержки на фактор производства (труд).

Предельную доходность труда можно представить как произведение предельной выручки на предельный продукт труда:

MRP_L = MR × MP_L

где

MR – предельная выручка,

MP_L – предельный продукт труда.

Фирма является монополистом на рынке блага и монопсонистом на рынке труда.

На рынке труда издержки фирмы на труд равны ставке заработной платы:

MIC_L = (TIC_L)’= (L×ω)’

По условию задачи известна функция предложения на труд

L = 0,2 × ω – 4,

отсюда

ω = 5 × L + 20

где

ω – ставка заработной платы,

L – количество нанимаемого труда.

MIC_L = (5 × L² + 20 × L)’= 10 × L + 20

Таким образом, для фирмы, являющейся монополистом на товарном рынке и монопсонистом на рынке труда условие максимизации прибыли при покупке фактора производства будет иметь вид:

MR × MP_L = MIC_L

Найдём предельную выручку как производную от общей выручки:

MR = TR’ = (P×Q)’ = (100 × Q – Q²)’=100 – 2 × Q

где

Р = 100 – Qd – обратная функция спроса.

По условию Q = 5 × L, следовательно,

MR = 100 – 10 × L.

Найдём предельный продукт труда:

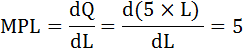
Воспользуемся условием максимизации прибыли и найдём количество закупаемого фактора:

(100 – 10 × L) × 5 = 10 × L + 20

500 – 50 × L = 10 × L + 20

480 = 60 × L

L = 8

Объём продукции выпускаемой фирмой:

Q = 5 × 8 = 40

Фирма будет продавать продукцию по цене

Р = 100 – 40 = 60.

Задача № 7. Оценка будущих доходов от инвестиций

Инвестиционный проект требует первоначальных вложений в размере 18 000 ден.ед. Через 1 год доходы составят 11 000 ден.ед., к концу 2-го года 12 650ден.ед. Выгодно ли осуществить данный проект, если i=10%,i=15%?

Решение:

Рассчитаем чистую дисконтированную стоимость (Net Present Value) проекта по формуле:

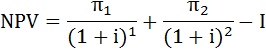
где

I – инвестиции,

π_n – прибыль, получаемая в n году,

i – норма дисконта (ставка процента).

При i = 10%:

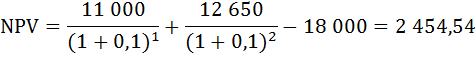
При i = 15%:

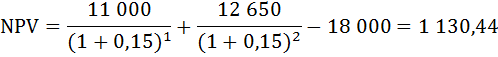
NPV ˃ 0

Это значит, что приведённая прибыль, ожидаемая от инвестиций больше, чем величина произведённых инвестиций.

Данный проект осуществлять выгодно при любой ставке процента.

Задача № 8. Расчёт цены акции

Годовая ставка процента i = 10%. Рассчитать, как оценивается акция в настоящий момент, если она приносит ежегодно 100 рублей в течение 5 лет, а потом погашается по номиналу за 1 000 рублей.

Решение:

Принцип расчёта цены акции основан на дисконтировании будущих доходов, которые будут по ней выплачены.
Курс акции равен:

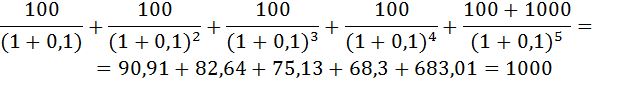
Задача № 9. Расчёт приведённой стоимости

Две фирмы предлагают проекты строительства дома отдыха. Первая берётся построить его за два года и просит в первом году 200 млн р., а в начале второго – 300 млн р. Вторая фирма нуждается в трёхлетних инвестициях: 90, 180 и 288 млн р. в начале каждого года соответственно.

а) Какой из этих проектов дешевле, если для сравнения использовать 20 %-ную ставку дисконтирования? Найти приведённые стоимости проектов.

б) Какой из этих проектов дешевле, если для сравнения использовать 10%-ную ставку дисконтирования? Найти приведённые стоимости проектов.

г) Найти так называемую уравнивающую ставку дисконтирования, при котором ни одному из проектов нельзя отдать предпочтение.

Решение:

Рубль сегодня больше чем рубль через год. Поэтому затраты равные одному рублю сегодня больше, чем затраты, равные одному рублю завтра. Для того чтобы узнать общую сумму затрат за несколько периодов времени, необходимо привести затраты за ряд периодов (лет) в эти проекты к одному моменту времени.

а) Пусть r = 20%. Найдём приведённую стоимость проектов по формуле:

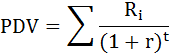
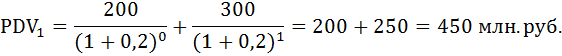
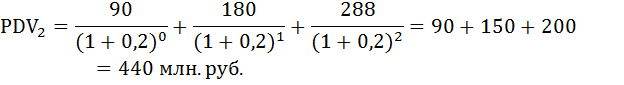
При ставке дисконтирования равной 20% проект второй фирмы оказался дешевле.

б) Пусть r = 10%. Найдём приведённую стоимость проектов:

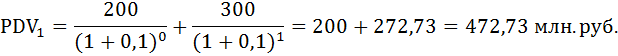
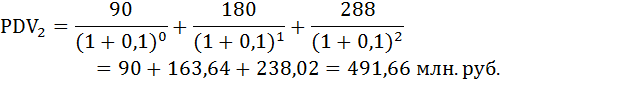
При ставке дисконтирования 10% первый проект оказался дешевле.

в) Найдём уравнивающую ставку дисконтирования. Для этого решим уравнение:

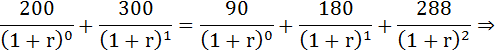
r = 0,1621 или 16,21%.

Задача № 10. Расчёт дисконтированного дохода

Если бы вам предложили на выбор два варианта:

а) получать 2600 ден. ед. каждый год до самой смерти;

б) получить 5000 ден. ед. через год, 8000 – в конце второго года и 20600 – в конце третьего года.

Ставка процента 10 %.

Какой из вариантов Вы предпочтете?

Решение:

Поскольку число жизни не известно, то при ставке 10% по варианту а) дисконтированный доход составит не более 26000 ден. ед.:

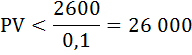
По варианту б) дисконтированный доход составит:

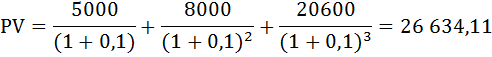
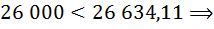
 выгоднее второй вариант.